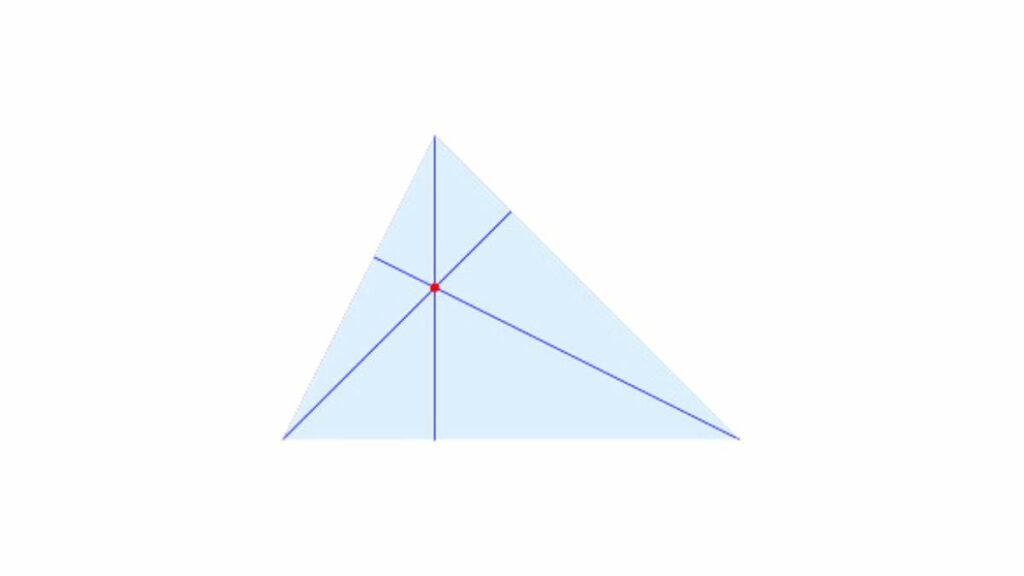
Punti notevoli: ortocentro del triangolo
Quando si studiano i punti notevoli il primo da memorizzare è l’ortocentro del triangolo. Si tratta di un punto che può essere sia interno che esterno alla figura a seconda delle sue caratteristiche, ovvero lati e angoli. Per trovarlo occorre disegnare le tre altezze della figura, ciascuna relativa a uno dei lati.
A seconda che il triangolo sia isoscele, scaleno o equilatero la posizione di questo punto notevole cambia molto, così come per i suoi angoli interni.
Ci sono altri 4 punti notevoli dei triangoli. Vale a dire l’incentro (punto d’incontro delle bisettrici), il baricentro (intersezione delle mediane) e il circocentro (incontro degli assi).
Come si trova l’ortocentro del triangolo
Come accennato si tratta del punto di intersezione fra le altezze della figura. Trovarlo richiede quindi di disegnarle tutte e tre e prolungarle all’occorrenza. In alcuni triangoli infatti questo punto notevole non è interno alla figura e una volta tracciate le altezze fermandosi al punto di incontro con i lati non lo si trova ancora.
Per disegnare correttamente le altezze che si incontrano nell’ortocentro del triangolo è utile ripetere la loro definizione.
Si tratta del segmento perpendicolare condotto da un vertice della figura al lato opposto. Di solito si tracciano utilizzando le due squadre, una posizionata sul lato dove deve arrivare l’altezza e una che scorre fino a incontrare il vertice opposto.
Anche questi segmenti possono risultare sia interni che esterni al triangolo (basti pensare ai casi in cui la figura è ottusangola). In tal caso per riuscire a disegnare l’altezza bisogna anche prolungare il lato opposto al vertice da cui si sta partendo. Per indicare il punto di incontro una volta disegnate le tre linee si utilizza la lettera maiuscola O.
Per trovare la posizione esatta dell’ortocentro ci sono diversi modi, ma può aiutare riuscire a calcolare la lunghezza delle tre altezze. Se se ne conosce una e la misura dei lati è sufficiente calcolare la superficie del triangolo. A questo punto dividendolo per le misure degli altri due lati si trova la lunghezza delle altezze relative.
Dove si trova questo punto notevole in base ai lati
In base al tipo di figura a tre lati possiamo già capire molto sul punto d’incontro delle sue altezze:
- L’ortocentro del triangolo equilatero coincide con tutti gli altri suoi punti notevoli (baricentro, incentro, circocentro). Questo perché ognuna delle sue altezze è anche bisettrice del proprio angolo, nonché asse di simmetria e mediana del lato opposto. Per di più triangoli e lati di questa figura sono tutti congruenti fra di loto.
- Il punto di incontro delle altezze di un triangolo isoscele è sempre interno alla figura e si trova lungo l’altezza relativa alla base. La ragione è che questo segmento è in contemporanea altezza, bisettrice dell’angolo opposto alla base, asse di simmetria e mediana. Anche gli altri punti notevoli dei triangoli isosceli si trovano su questa linea.
- L’ortocentro del triangolo scaleno si trova sempre all’esterno della figura. Bisogna quindi prolungare le altezze oltre il punto d’incontro con il lato opposto fino a che non si trovano fra di loro. L’unica eccezione a questa regola è il triangolo rettangolo dove questo punto notevole coincide con il vertice opposto all’ipotenusa. Infatti entrambi i cateti sono altezze della figura.
Trovare la posizione dell’ortocentro del triangolo
Se in base alla tipologia di figura che abbiamo di fronte possiamo capire dove potrebbe trovarsi in modo approssimativo, si può fare un lavoro più preciso. Prendiamo come esempio un triangolo isoscele che abbia la base di 18 cm e i lati obliqui di 15 cm. Per prima cosa occorre trovare la misura dell’altezza relativa alla base, usando il teorema di Pitagora.
L’altezza è uno dei cateti del triangolo rettangolo formato da uno dei lati obliqui (l) e dalla metà della base (b/2).
Se si indica l’altezza con “h” bisogna quindi utilizzare la formula h =√l2 –(b/2)2. Quindi nel caso della figura che stiamo esaminando h = √152 – 92 = √225 – 81 = √144 = 12 cm.
A questo punto immaginando di disegnare le tre altezze si crea una seconda figura dove l’ortocentro del triangolo è uno dei vertici.
Il rapporto fra metà della base (b/2) e l’altezza h è uguale a quello che b/2 ha con il segmento che unisce l’ortocentro O alla base. Chiamando il triangolo ABC con A come vertice opposto alla base BC possiamo indicare b/2 come BH, l’altezza con AH e la distanza dell’ortocentro dalla base OH.
Abbiamo già detto che O si trova lungo l’altezza relativa alla base nei triangoli isosceli.
Scriveremo perciò AH : BH = BH : OH.
AH è h quindi 12 cm e BH come già detto è lungo 9 cm. Risolvendo la proporzione viene quindi OH = BH x BH/AH = BH2/AH = 81/12 = 6,75 cm.